Rigid-body registration

Find the rigid-body transformation that aligns two sets of points. Part of pipeline for multiple recordings.

Consistent cartographic projections across multiple recordings

In notebook 2 we saw how to do tissue cartography on a single volumetric image. But often, we have multiple images of very similarly shaped objects - either the successive frames of a movie or multiple recordings of biological structures with very consistent shapes, like the Drosophila egg. We want to use “the same” UV map/cartographic projection for all of the images - both so that we don’t need to redo the work of creating the UV map, and so that positions in our cartographic projections always correspond to the same anatomical position on the imaged object (e.g. the anterior side of the Drosophila embryo is always left, and the dorsal midline corresponds to the line \(v=1/2\) in UV space).

To do this, we use mesh registration. The idea is that we have a reference mesh - for example, from the first frame of a movie - on which a UV map is defined. We then move and deform this mesh so that it fits our target mesh - which describes the surface we want to extract from the volumetric data - as well as possible. The registered reference mesh now fits the volumetric data but still carries the UV map, and can now be used to create a cartographic projection.

If you have a consistently shaped object that you know you will image many times - in the Streichan lab, the early Drosophila embryo, of which we have hundreds of in toto recordings - it might make sense to make an idealized “prototypical” mesh with a nice mesh and UV map, that you can use as a reference.

Mesh/point cloud registration and deformation are very well-studied problems and we can make use of many robust and already-implemented algorithms. We proceed in two steps: 1. Affine registration: Align reference mesh to target mesh using translations, rotations, and possible rescaling, for instance by Iterative Closest Point. 2. Wrapping: Move each point on the registered reference mesh to the closest point on the surface defined by the target mesh.

Here we deal with step 1. You can also use the pymeshlab GUI.

For step 2, look at the wrapping module. You can also “wrap” interactively in blender, using the shrinkwrap modifier.

Loading the example dataset

We will use the same dataset - a Drosophila example - as in the Tutorial “Tissue cartography for a non-trivial topology”.

metadata_dict = {'filename': 'datasets/registration_example/Drosophila_CAAX-mCherry',
                 'resolution_in_microns': (1.05, 1.05, 1.05), # lightsheet data has isotropic resolution
                 'subsampling_factors': (1/2, 1/2, 1/2),
                }

image = tcio.adjust_axis_order(tcio.imread(f"{metadata_dict['filename']}.tif"))
print("image shape:", image.shape) # image shape - spatial axes are in z-x-y order

image shape: (1, 190, 509, 188)

Load a 3d segmentation of embryo

# after creating an ilastik project, training the model, and exporting the probabilities, we load the segmentation

segmentation = tcio.read_h5(f"{metadata_dict['filename']}_subsampled-image_Probabilities.h5")
segmentation = segmentation[0] # Select the first channel of the segmentation - it's the probability a pixel
                               # is part of the sample
print("segmentation shape:", segmentation.shape)

segmentation shape: (95, 254, 94)

# look at the segmentation in a cross section

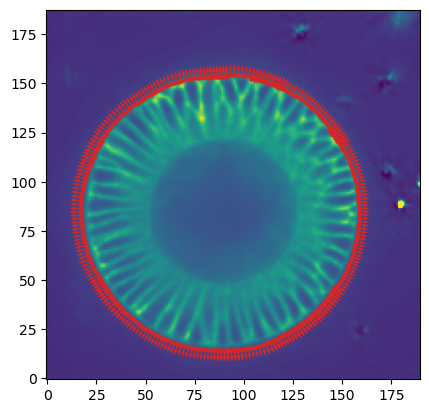
plt.imshow(segmentation[:,:,50], vmin=0, vmax=1)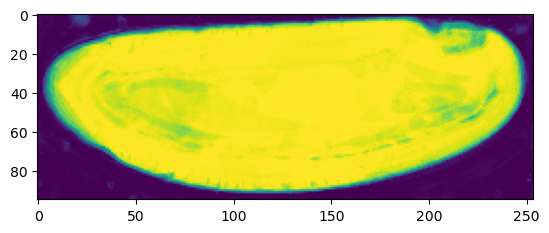

Meshing

Using the marching cubes method.

# Now we create a 3d mesh using the marching cubes method

vertices, faces = tcremesh.marching_cubes(segmentation, 0.5, sigma_smoothing=0.5)

# EXTREMELY IMPORTANT - we now rescale the vertex coordinates so that they are in microns.
vertices_in_microns = vertices * (np.array(metadata_dict['resolution_in_microns'])
                                 /np.array(metadata_dict['subsampling_factors']))

mesh = tcmesh.ObjMesh(vertices_in_microns, faces)
mesh.name = "Drosophila_CAAX-mCherry_mesh_marching_cubes"
mesh.write_obj(f"{metadata_dict['filename']}_mesh_marching_cubes.obj")

# improve mesh quality using meshlab
ms = pymeshlab.MeshSet()
ms.load_new_mesh(f"{metadata_dict['filename']}_mesh_marching_cubes.obj")
ms.meshing_isotropic_explicit_remeshing()
ms.save_current_mesh(f"{metadata_dict['filename']}_mesh_remeshed.obj")

Registration

In the data folder, we have the mesh we just created, Drosophila_CAAX-mCherry_mesh_remeshed.obj, as well as out reference mesh Drosophila_reference.obj - an idealized Drosophila embryo with a standardized UV mapping, corresponding to a cylindrical projection. You can look at both meshes in the blender file Drosophila_reference.blend (where I recentered the mesh from the image data - which you should not do if you want to use it for interpolation!).

Our goal will now be to register the reference mesh and the deformed mesh using an affine transformation. Affine transformations are generally written as 4d-matrices, with the extra dimension allowing to save the translation as part of the matrix.

Affine registration proceeds in two parts. First, we get an initial guess by matching the centroid and axes of inertia of the source and target mesh. Then we refine the registration using the iterative closest point algorithm. For all calculations, we make use of the KDTree data structure which allows efficient lookup of the closest point from a given point cloud to a query point.

source

align_by_centroid_and_intertia

 align_by_centroid_and_intertia (source, target, q=0, scale=True,
                                 shear=False, n_samples=10000,
                                 choose_minimal_rotation=False)

*Align source point cloud to target point cloud using affine transformation.

Align by matching centroids and axes of inertia tensor. Since the inertia tensor is invariant under reflections along its principal axes, all 2^3 reflections are tried and (a) the one leading to the best agreement with the target or (b) the one corresponding to the least amount of rotation is chosen. This is controlled using the choose_minimal_rotation argument.*

	Type	Default	Details
source	np.array of shape (n_source, 3)		Point cloud to be aligned.
target	np.array of shape (n_target, 3)		Point cloud to align to.
q	int	0	Quantile for outlier removal. Removes points with coordinates outside (qth, (1-1)qth) quantile from calculation of inertia tensor and centroid
scale	bool	True	Whether to allow scale transformation (True) or rotations only (False)
shear	bool	False	Whether to allow shear transformation (True) or rotations/scale only (False)
n_samples	int	10000	Number of samples of source to use when estimating distances.
choose_minimal_rotation	bool	False	Whether to chose the rotation matrix closest to the identity. If False, the rotation matrix (possibly with det=-1) leading to the best alignment with the target is chosen.
Returns	np.array, np.array		affine_matrix_rep : np.array of shape (4, 4) Affine transformation source -> target aligned : np.array of shape (n_source, 3) Aligned coordinates

source

get_inertia

 get_inertia (pts, q=0)

Get inertia tensor of 3d point cloud. q in [0, 1) removes points with outlier coordinates.

source

package_affine_transformation

 package_affine_transformation (matrix, vector)

Package matrix transformation & translation into (d+1,d+1) matrix representation of affine transformation.

mesh_data = tcmesh.ObjMesh.read_obj(f"{metadata_dict['filename']}_mesh_remeshed.obj")
mesh_ref = tcmesh.ObjMesh.read_obj(f"datasets/registration_example/Drosophila_reference.obj")

# For illustration purposes, let's rotate and scale the reference mesh so it's off
random_rotation = stats.special_ortho_group.rvs(3)
mesh_ref.vertices = 1.1 * mesh_ref.vertices @ random_rotation
mesh_ref.normals = mesh_ref.normals @ random_rotation

Warning: readOBJ() ignored non-comment line 4:
  o embryo_rect

# let's test this function

q = 0.0

trafo_centroid_intertia, vs_prealigned = align_by_centroid_and_intertia(mesh_ref.vertices,
                                                                        mesh_data.vertices,
                                                                        q=q, scale=True, shear=True,
                                                                        choose_minimal_rotation=True)
data_centroid = stats.trim_mean(mesh_data.vertices, q, axis=0)
data_inertia = get_inertia(mesh_data.vertices, q=q)
data_eig = np.linalg.eigh(data_inertia)

ref_centroid = stats.trim_mean(mesh_ref.vertices, q, axis=0)
ref_inertia = get_inertia(mesh_ref.vertices, q=q)
ref_eig = np.linalg.eigh(ref_inertia)

prealigned_centroid = stats.trim_mean(vs_prealigned, q, axis=0)
prealigned_inertia = get_inertia(vs_prealigned, q=q)
prealigned_eig = np.linalg.eigh(prealigned_inertia)

prealigned_eig.eigenvalues, data_eig.eigenvalues

(array([ 3141.61049685,  3229.00962125, 19280.74388138]),
 array([ 3141.61049685,  3229.00962125, 19280.74388138]))

# we correctly matched the axes of intertia and the centroids

prealigned_eig.eigenvalues / data_eig.eigenvalues, np.linalg.norm(data_centroid - prealigned_centroid)

(array([1., 1., 1.]), 1.3012829303080923e-12)

prealigned_eig.eigenvectors, data_eig.eigenvectors

(array([[-0.40234803,  0.91474904, -0.03674582],
        [-0.03532074,  0.02459749,  0.99907328],
        [ 0.91480518,  0.40327305,  0.02241286]]),
 array([[-0.40234803,  0.91474904, -0.03674582],
        [-0.03532074,  0.02459749,  0.99907328],
        [ 0.91480518,  0.40327305,  0.02241286]]))

# mean distance to closest target

tree = spatial.cKDTree(mesh_data.vertices)
np.mean(tree.query(mesh_ref.vertices)[0]), np.mean(tree.query(vs_prealigned)[0])

(147.54268012467426, 6.674543338122944)

_ = align_by_centroid_and_intertia(mesh_ref.vertices, mesh_data.vertices, q=q, scale=False)

151 ms ± 15.1 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)

# We now save the pre-registered mesh. Note that we want to transform both our
# mesh coordinates and the corresponding normals, as well as potentially flip face orientation

mesh_registered = mesh_ref.apply_affine_to_mesh(trafo_centroid_intertia)
mesh_registered.name = "Drosophila_reference_preregistered"
mesh_registered.write_obj(f"datasets/registration_example/Drosophila_reference_preregistered.obj")

for i in range(10):
    if i % 2 == 0:
        continue
    print(i)

Iterative closest point algorithm

We can refine the initial registration with the ICP algorithm. This code is based on igl.procrustes and trimesh.registration.

source

procrustes

 procrustes (source, target, include_scaling=True,
             include_reflections=True)

*Wrapper around igl.procrustes

Compute rotation+scaling+translation between two sets of points.*

	Type	Default	Details
source	np.array of shape (n_points, n_dimensions)
target	np.array of shape (n_points, n_dimensions)
include_scaling	bool	True
include_reflections	bool	True
Returns	np.array, np.array, float		trafo_affine : np.array (4,4) array representing the affine transformation from source to target. aligned : np.array The orientation of the source that best fits the target. disparity : float np.linalg.norm(aligned-target, axis=1).mean()

mesh_ref = tcmesh.ObjMesh.read_obj(f"datasets/registration_example/Drosophila_reference.obj")

source = np.copy(mesh_ref.vertices)
target = 1.3*mesh_ref.vertices@ stats.special_ortho_group.rvs(3) + np.array([12,12,1000])

trafo_affine, transformed, cost = procrustes(source, target)
trafo_affine, cost

Warning: readOBJ() ignored non-comment line 4:
  o embryo_rect

(array([[  -1.27176709,    0.2129668 ,   -0.16508667,   12.        ],
        [   0.24407945,    1.24790943,   -0.27045754,   12.        ],
        [   0.11416518,   -0.29557943,   -1.26079305, 1000.        ],
        [   0.        ,    0.        ,    0.        ,    1.        ]]),
 3.4643816882932517e-12)

spatial.procrustes(source, target)

(array([[-0.00002796,  0.00649897, -0.00003995],
        [ 0.00026319,  0.00643907, -0.00003871],
        [ 0.00042143,  0.00637917, -0.00003618],
        ...,
        [ 0.000204  , -0.00637917,  0.00000789],
        [ 0.0001068 , -0.00643907,  0.00000707],
        [-0.00005934, -0.00649897,  0.00000636]]),
 array([[-0.00002796,  0.00649897, -0.00003995],
        [ 0.00026319,  0.00643907, -0.00003871],
        [ 0.00042143,  0.00637917, -0.00003618],
        ...,
        [ 0.000204  , -0.00637917,  0.00000789],
        [ 0.0001068 , -0.00643907,  0.00000707],
        [-0.00005934, -0.00649897,  0.00000636]]),
 2.1869379044888485e-28)

/opt/hostedtoolcache/Python/3.10.16/x64/lib/python3.10/site-packages/fastcore/docscrape.py:230: UserWarning: potentially wrong underline length... 
Returns 
---------- in 
Apply the iterative closest point algorithm to align point cloud a with
point cloud b. Will only produce reasonable results if the...
  else: warn(msg)

source

icp

 icp (source, target, initial=None, threshold=0.0001, max_iterations=20,
      include_scaling=True, n_samples=1000)

Apply the iterative closest point algorithm to align point cloud a with point cloud b. Will only produce reasonable results if the initial transformation is roughly correct. Initial transformation can be found by applying Procrustes’ analysis to a suitable set of landmark points (often picked manually), or by inertia+centroid-based alignment, implemented in align_by_centroid_and_intertia.

	Type	Default	Details
source	(n,3) float		Source points in space.
target	(m,3) float or Trimesh		Target points in space or mesh.
initial	NoneType	None	Initial transformation.
threshold	float	0.0001	Stop when the change in cost is less than threshold
max_iterations	int	20	Maximum number of iterations
include_scaling	bool	True	Whether to allow dilations. If False, orthogonal Procrustes is used
n_samples	int	1000	If not None, n_samples sample points are randomly chosen from the source array for distance computation
Returns	np.array, np.array, float		matrix : (4,4) np.array The transformation matrix sending a to b transformed : (n,3) np.array The image of a under the transformation cost : float The cost of the transformation

mesh_data = tcmesh.ObjMesh.read_obj(f"{metadata_dict['filename']}_mesh_remeshed.obj")
mesh_ref = tcmesh.ObjMesh.read_obj(f"datasets/registration_example/Drosophila_reference.obj")

# for illustration purposes, let's rotate and scale the reference mesh so it's off
mesh_ref = mesh_ref.apply_affine_to_mesh(1.1 * stats.special_ortho_group.rvs(3))

Warning: readOBJ() ignored non-comment line 4:
  o embryo_rect

source = np.copy(mesh_ref.vertices)
target = np.copy(mesh_data.vertices)
tree = spatial.cKDTree(target)

np.mean(tree.query(source)[0])

135.49963003678982

trafo_initial, prealigned = align_by_centroid_and_intertia(source, target, q=0, scale=True, shear=True)

trafo_initial

array([[ -0.06,  -0.6 ,   0.73,  91.62],
       [ -0.47,  -0.53,  -0.47, 270.93],
       [ -0.81,   0.49,   0.27,  93.89],
       [  0.  ,   0.  ,   0.  ,   1.  ]])

np.mean(tree.query(prealigned)[0])

6.2561533646459395

trafo_icp, icp_aligned, cost = icp(source, target, initial=trafo_initial, threshold=1e-4, max_iterations=50,
                                   include_scaling=True, n_samples=1000)

np.mean(tree.query(icp_aligned)[0])

5.8583626546496586

trafo_icp

array([[ -0.05039776,  -0.61739046,   0.73713584,  92.41686432],
       [ -0.47081468,  -0.54148091,  -0.48110009, 263.05296811],
       [ -0.82768076,   0.48507969,   0.28067945,  94.25355359],
       [  0.        ,   0.        ,   0.        ,   1.        ]])

Registration in MeshLab

You can also perform registration graphically in MeshLab - see this tutorial: https://www.youtube.com/watch?v=30bJcj6yA4c. Use this if you have problems with the automated method above.

Wrapping

Now that we have registered the mesh, we can wrap it! Let’s first do it using Blender with the shrinkwrap modifier. Go to the “layout” tab and click the “blue wrench” on the right to add a modifier. Search for shrinkwrap, select the target, and use “Tangent Normal Project” for best results:

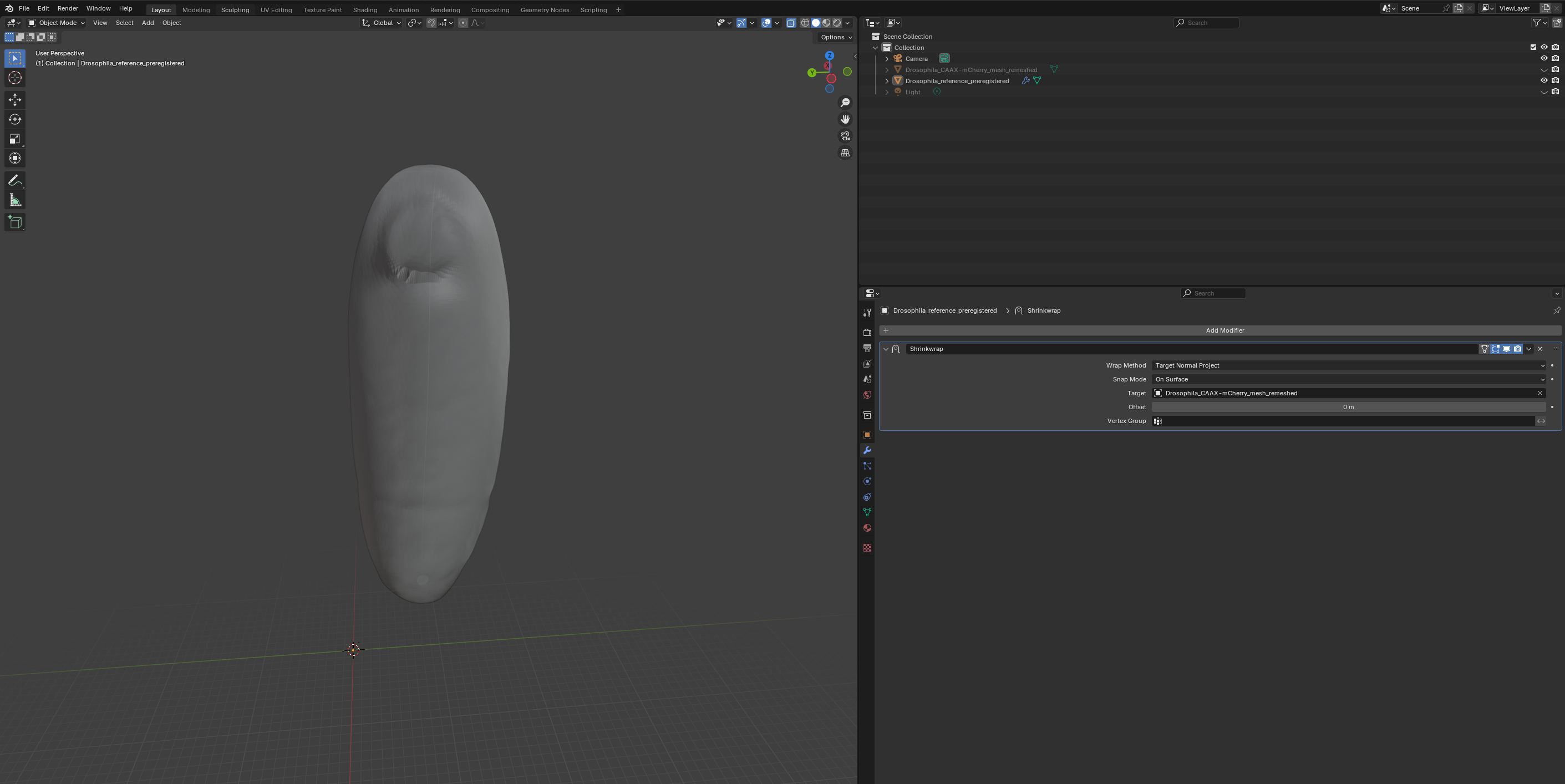
If things look good, click “Apply” to make the modifier permanent and export the mesh as Drosophila_reference_wrapped.obj.

Normals and normal-related problems

This may be a good point to note that if you have any problems with multilayer projections, your normals may be messed up. Some advice on how to visualize and if necessary, recalculate mesh normals.

Useful tools: “Recalculate normals” (under “Mesh” in “Edit Mode”), and the modifier “Normals -> Weighted Normal” (smoothes normals) and “Deform -> Smooth”.

image = tcio.adjust_axis_order(tcio.imread(f"{metadata_dict['filename']}.tif"))
mesh = tcmesh.ObjMesh.read_obj(f"datasets/registration_example/Drosophila_reference_wrapped.obj")
resolution = metadata_dict["resolution_in_microns"]

Warning: readOBJ() ignored non-comment line 4:
  o Drosophila_reference_wrapped_smoothed_normals

slice_image, slice_vertices, slice_normals = tcinterp.get_cross_section_vertices_normals(1, 100,
                                image, mesh, metadata_dict["resolution_in_microns"], width=1.5)

plt.scatter(*slice_vertices.T, s=5, c="tab:red")
plt.quiver(*slice_vertices.T, *slice_normals.T, color="tab:red")

plt.imshow(slice_image[0], vmax=10000, origin="lower")

Procedural wrapping

Of course, we do not want to have to do this by hand for a movie with \(\sim100\) frames! In the wrapping module we will introduce tools to automate the wrapping process.

UV projection

To see how well all of this has worked, let’s use the wrapped mesh to generate UV projections. We will compare it with the automatic sphere unwrap on the original data mesh.

normal_offsets = np.array([-4, -2, 0, 2]) ##np.linspace(-5, 2, 8) # in microns
metadata_dict["normal_offsets"] = normal_offsets # add the info to the metadata
uv_grid_steps = 512

tcio.save_dict_to_json(f"{metadata_dict['filename']}_metadata.json", metadata_dict)

projected_data_wrapped, projected_coordinates_wrapped, projected_normals_wrapped = tcinterp.create_cartographic_projections(
    image=f"{metadata_dict['filename']}.tif",
    mesh=f"datasets/registration_example/Drosophila_reference_wrapped.obj",
    resolution=metadata_dict["resolution_in_microns"],
    normal_offsets=normal_offsets,
    uv_grid_steps=uv_grid_steps)

Warning: readOBJ() ignored non-comment line 4:
  o Drosophila_reference_wrapped_smoothed_normals
/home/nikolas/Documents/UCSB/streichan/numerics/code/python code/jupyter notebooks/blender-tissue-cartography/blender_tissue_cartography/interpolation.py:215: RuntimeWarning: UV map has self-intersections, 111104 flipped triangles. Try use_fallback=True?
  warnings.warn("UV map has self-intersections, {} flipped triangles. Try use_fallback=True?".format(

projected_data, projected_coordinates, projected_normals = tcinterp.create_cartographic_projections(
    image=f"{metadata_dict['filename']}.tif",
    mesh="datasets/registration_example/Drosophila_CAAX-mCherry_mesh_remeshed_sphere_uv.obj",
    resolution=metadata_dict["resolution_in_microns"],
    normal_offsets=normal_offsets,
    uv_grid_steps=uv_grid_steps)

Warning: readOBJ() ignored non-comment line 4:
  o Drosophila_CAAX-mCherry_mesh_remeshed
/home/nikolas/Documents/UCSB/streichan/numerics/code/python code/jupyter notebooks/blender-tissue-cartography/blender_tissue_cartography/interpolation.py:215: RuntimeWarning: UV map has self-intersections, 8 flipped triangles. Try use_fallback=True?
  warnings.warn("UV map has self-intersections, {} flipped triangles. Try use_fallback=True?".format(

fig, (ax1, ax2) = plt.subplots(figsize=(8,8), ncols=2)
ax1.imshow(projected_data_wrapped[0, 0], vmax=10000)
ax2.imshow(projected_data[0, 0][::-1,::-1].T, vmax=10000)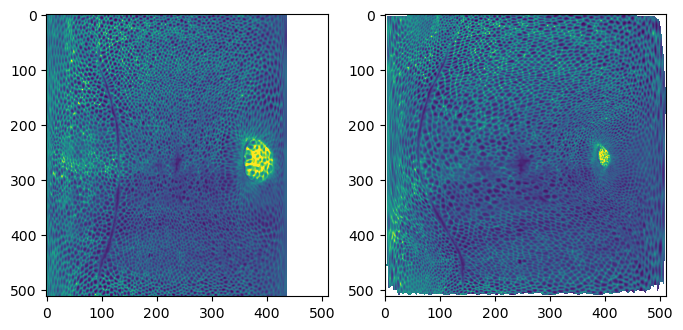

# save images for visualization in blender
texture_path = f"{os.getcwd()}/{metadata_dict['filename']}_textures"
tcio.save_stack_for_blender(projected_data_wrapped, texture_path, normalization=(0.01, 0.99))

# save images as .tif stack for analysis
tcio.save_for_imageJ(f"{metadata_dict['filename']}_projected.tif", projected_data_wrapped, z_axis=1)
tcio.save_for_imageJ(f"{metadata_dict['filename']}_3d_coordinates.tif", projected_coordinates_wrapped)
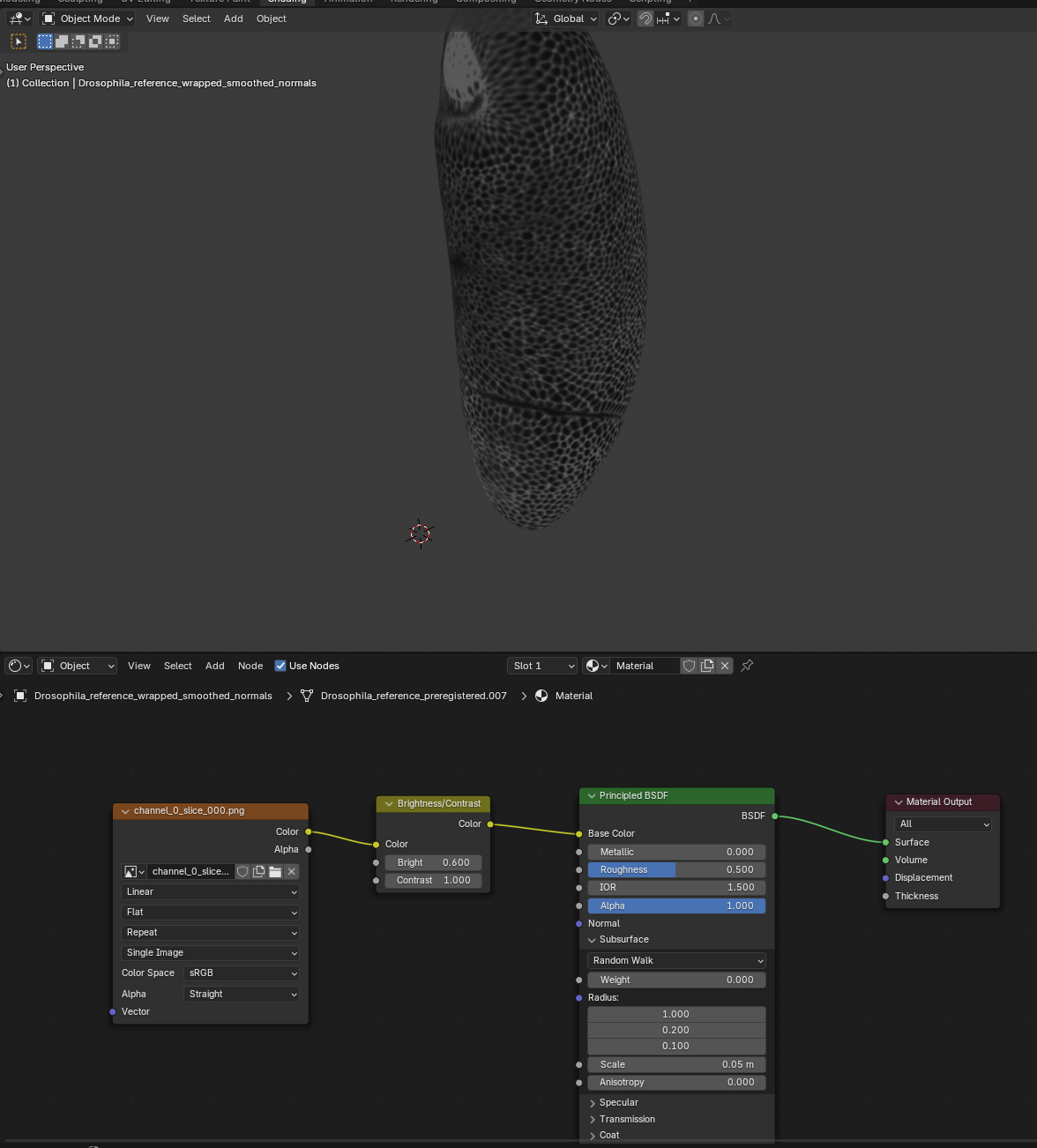
tcio.save_for_imageJ(f"{metadata_dict['filename']}_normals.tif", projected_normals_wrapped)

Let’s add a shader to check the texture looks good: